Matriz (matemática)
Em matemática, uma matriz m X n é uma tabela de m linhas e n colunas de símbolos sobre um conjunto, normalmente um corpo, F, representada sob a forma de um quadro s. As matrizes são muito utilizadas para a resolução de sistemas de equações lineares e transformações lineares
As linhas horizontais da matriz são chamadas de linhas e as linhas verticais são chamadas de colunas. Logo uma matriz com m linhas e n colunas é chamada de uma matriz m por n (escreve-se m×n) e m e n são chamadas de suas dimensões, tipo ou ordem. Por exemplo, a matriz a seguir é uma matriz de ordem 2×3 com elementos naturais
Um elemento de uma matriz A que está na i-ésima linha e na j-ésima coluna é chamado de elemento i,j ou (i,j)-ésimo elemento de A. Ele é escrito como ai,j ou a[i,j]. Nesse exemplo, o elemento a1 2 é 2, o número na primeira linha e segunda coluna do quadro.
As entradas (símbolos) de uma matriz também podem ser definidas de acordo com seus índices i e j. Por exemplo,  para i de 1 a 3 e j de 1 a 2, define a matriz 3x2
para i de 1 a 3 e j de 1 a 2, define a matriz 3x2 
Nas linguagens de programação, os elementos da matriz podem estar indexados a partir de 1 (Fortran, MATLAB, R, etc) ou a partir de 0 (C e seus dialetos). Por exemplo, o elemento a(1,1) em Fortran corresponde ao elemento a[0][0] em C.
Multiplicação por um escalar
A multiplicação por um escalar é uma das operações mais simples que podem ser feitas com matrizes. Para multiplicar um número k qualquer por uma matriz n×m A, basta multiplicar cada entrada aij de A por k. Assim, a matriz resultante B será também n×m e bij = k.aij. Com isso, pode-se pensar também na noção de dividir uma matriz por um número: basta multiplicá-la pelo inverso desse número. Mas essa noção pode ser perigosa: enquanto a multiplicação entre um número e uma matriz pode ser dita "comutativa", o mesmo não vale para a divisão, pois não se pode dividir um número por uma matriz.
Por exemplo:
Adição e subtração entre matrizes
Dado as matrizes A e B do tipo m por n, sua soma A + B é a matriz m por n computada adicionando os elementos correspondentes: (A + B)[i,j] = A[i, j] + B[i,j].
Por exemplo:
Para melhorar a forma de calcular, você pode reescrever a segunda matriz, revertendo seus elementos, onde o elemento (-1) passará para (1) e o elemento (2) passará para (-2) e assim sucessivamente. Após feito isso, além de fazer A-B, você usará A+B.
Lembre-se: Você só pode fazer isso com Matriz negativa, onde recebe o sinal negativo, por exemplo: em -A+B, o A que poderá ser reescrito.
Multiplicação de matrizes
Multiplicação de duas matrizes é bem definida apenas se o número de colunas da matriz da esquerda é o mesmo número de linhas da matriz da direita. Se A é uma matriz m por n e B é uma matriz n por p, então seu produto AB é a matriz m por p (m linhas e p colunas) dada por:
para cada par i e j.
Por exemplo:
É importante notar que a comutatividade não é garantida; isto é, dadas as matrizes A e B com seu produto definido, então geralmente AB ≠ BA.



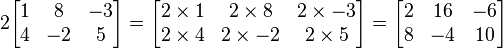
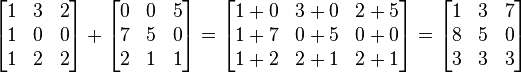
![(AB)[i,j] = A[i,1] B[1,j] + A[i,2] B[2,j] + ... + A[i,n] B[n,j]](https://upload.wikimedia.org/math/c/0/9/c095cf66c12b7fcb599462becfbd3eaf.png)





